Question

Scores on the GRE (Graduate Record Examination) are normally distributed with a mean of 513 and a standard deviation of 82. Use the 68-95-99.7 Rule to find the percentage of people taking the test who score between 513 and 759. The percentage of people taking the test who score between 513 and 759 is %

Answer 1

Note that we need calculate the scores between the mean (
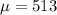`\mu=513`) and the mean plus 3 times the standard deviation. It is 3 times since the distance between the values given (513 and 759) divided by the standard deviation is 3 (
`(759-513)/(82)=3`)

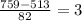So the rule say that 99.7% of data is between
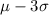`\mu - 3\sigma` and
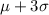`\mu + 3\sigma`, as it is a normal distribution half of 99.7% is between
`\mu` and
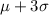`\mu+3\sigma`. Hence 49.85% of people score between 513 and 759.