Question

Find the annual percentage yield (APY) in the following situation. A bank offers an APR of 4.8% compounded daily. The annual percentage yield is %. (Do not round until the final answer. Then round to two decimal places as needed.) Enter your answer in the answer box O Type here to search hp

Answer 1

4.92%

Explanation:

First of all, recall that if you increase a number C in x%, then you will have
`C+(x)/(100)C=C(1+(x)/(100))`

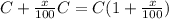
So increasing a number in x% is equivalent to multiply it by (1+x/100)

Now, suppose you have deposited $C where C is any amount > 0

If the bank offers an APR of 4.8% compounded daily, it means that your money increases
`(4.8)/(365)\%=(0.048)/(365)` daily.

So, after 365 days you will have

C multiplied by (1+0.048/365) 356 times, that is

(1)
`C(1+(0.048)/(365))^(365)=C((365.048)/(365))^(365)`

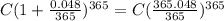
Now, you want to find a value x, such that C increased in x% equals the amount in (1).That would be the percentage your money increased in one year (APY)

`C((365.048)/(365))^(365)=C(1+(x)/(100))\Rightarrow x=100[((365.048)/(365))^(365)-1]`

Computing this amount, we get

x = 4.92 rounded to the nearest hundreth.

And the bank is offering an APY of 4.92%