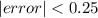Question

Let f(x)=x^2- 3. 1. Show that [0, 2] is a bracketing interval for f 2. Carry out 3 iterations of the bisection method applied to f with initial bracketing interval 0, 2]. Give your estimate for the root and the error bound

Answer 1

root estimate = 1.75

error bound = 0.25

Explanation:

f is a polynomial, so it is continuous in R (real numbers). Then you can use Bolzano's theorem.

f(0) = -3.1 < 0

f(2) = 4 - 3.1 = 0.9 > 0

Then there exists c in [0, 2], for which f(c) = 0

In the bisection method you generate a sequence
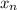`x_n` of approximations of a root. If you have a bracketing interval [a, b], such that

f(a) and f(b) have opposite signs, then you use approximate the root as
`x_n = (a+b)/(2)`

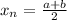
In this case:

`x_0 = 1`

`f(0)<0\\f(1)<0\\f(2)>0`

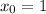
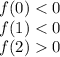
Then:

`x_1=1.5\\f(1.5)<0\\f(2)>0\\`

`x_2= ((1.5 + 2))/(2)= 1.75`

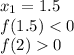
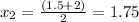
The error bound is half the width of the interval [1.5, 2]

`|error| < 0.25`