Question

Let ABC be a right triangle with legs AB = 8 cm and AC = 9 cm. What is the largest possible area of a rectangle ADEF if the points D, E and F belong to the sides AB, BC and CA, respectively?

Answer 1

The largest possible area would be 18 square cm.

Explanation:

Given,

ABC is a right triangle,

Having legs,

AB = 8 cm, AC = 9 cm,

Also, points D, E and F belong to the sides AB, BC and CA, respectively

Such that we obtain a rectangle ADEF,

Since, Δ BDE is similar to Δ BAC,

( by AA similarity postulate, because ∠BDE ≅ ∠BAC, both are right angles and ∠DBE ≅ ∠ABC, both are same angles )

∵ Corresponding sides of similar triangle are proportional,

I.e.
`(BD)/(AB)=(DE)/(AC)`

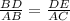
Let AD = x ⇒ BD = 8 - x

By substituting the values,

`(8-x)/(8)=(DE)/(9)`

`\implies DE=(9)/(8)(8-x)`

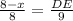
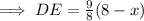
Thus, the area of the rectangle ADEF would be,

`A(x) = AD* DE`

`\implies A(x) = x((9)/(8)(8-x))=(9)/(8)(8x-x^2)`

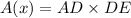
Differentiating with respect to x,

`A'(x) = (9)/(8)(8-2x)`

Again differentiating w.r.t. x,

`A''(x) = (9)/(8)(-2)=-(9)/(4)`

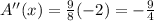
For maxima or minima,

A'(x) = 0

`\implies (9)/(8)(8-2x)=0`

`\implies 8-2x=0`

`\implies x = 4`

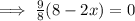
At x = 4, A''(x) = negative,

Hence, the area would be maximum if x = 4,

The maximum area of the rectangle ADEF,

`A(4) = (9)/(8)(8* 4-(4)^2)=(9)/(8)(32-16)=(9)/(8)* 16=9* 2=18\text{ square cm}`