Question

The position of a moving particle is given as Ř = (2t + 1,t^2 – 3) (meter), where t is time in second. Find the velocity of the particle at t = 1 (sec).

Answer 1

Veocityl=(2,2)

speed=
`2\sqrt[2]{2}` m/s

Step-by-step explanation:

To solve this problem, the first thing we do is find the velocity vector by deriving the position vector with respect to time, since velocity is known as the change of position with respect to time

R=(2t + 1,t^2 – 3)

`(dR)/(dt) =v=(2,2t)\\`

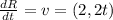
we evaluate the vector at t = 1s

v=(2,2t)

v=(2,2(1))

v=(2,2)

the velocity vector is (2,2) m / s

if what we want to find is speed, we find the magnitude of the vector as follows

V=
`\sqrt[2]{x^(2)+ y^2} =\sqrt[2]{2^(2)+ 2^2}=2√(2)`m/S