Question

When is a Polytropic expansion/compression (PV^n=C) process reversible (for which values of n? ) and why?

Answer 1

When n is gamma:
`n = \gamma= \cfrac{C_p}{C_v}`

Also known as the heat capacity ratio.

Step-by-step explanation:

For an ideal gas of constant heat capacity, if we want an adiabatic process, that is, a process in which there is no entropy change, we will have the following relation:

`dU = T dS - Pd V\\dS= 0 \implies  dU= -PdV`

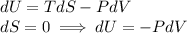
But we also know that
`dU = C_v dT`

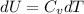
Moreover, we have by the ideal gas law:

`PV= NR\, T\\VdP + PdV = NR \, dT`

Now, if we eliminate dT from the last equations, we get:

`VdP + P dV = NR\,  \Big( -\cfrac{P dV}{C_v}\Big)`

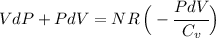
If we act algebraically on this, we get:

`\Big( 1 + \cfrac{NR}{C_v} \Big) \cfrac{dV}{V}+ \cfrac{dP}{P}=0`

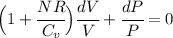
Now, the coeffcient on the left :

`1 + \cfrac{NR}{C_v} = \cfrac{C_v+NR}{C_v } = \cfrac{C_p}{C_v} = \gamma`

Where we have made use of so called Mayer's relation for an ideal gas:

`C_p= C_v + NR`

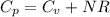
Going back to our last equation, we find:

`\gamma \cfrac{dV}{V}+ \cfrac{dP}{P}=0\\`

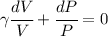
We can integrate this and get:

`\gamma \ln V + \ln P = K\\\ln (P\, V ^\gamma ) = K\\\\PV^\gamma = C`

Where K and C are just integration constants.