Question

A fluid has a dynamic viscosity of 0.048 Pa.s and a specific gravity of 0.913. For the flow of such a fluid over a flat solid surface, the velocity at a point 75 mm away from the surface is 1.125 m/s. Calculate the shear stress at a point 50 mm away from the solid surface if the velocity distribution of the fluid can be represented by a parabolic velocity profile with the vertex of the parabola at a point 75 mm away from the surface where the velocity is 1.125 m/s? The general equation of parabola can be assumed to be: V = A + By + Cy2 , where A, B, and C are constants.

Answer 1

Step-by-step explanation:

First we should recall how Newton's laws relates shear stress to a fluid's velocity profile:

`\tau = \mu \cfrac{\partial v}{\partial y}`

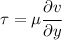
where tau is the shear stress, mu is viscosity, v is the fluid's velocity and y is the direction perpendicular to flow.

Now, in this case we have a parabolic velocity profile, and also we know that the fluid's velocity is zero at the boundary (no-slip condition) and that the vertex (maximum) is at
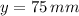`y=75 \, mm` and the velocity at that point is
`1.125 \, m/s`

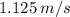
We can put that in mathematical terms as:

`v(y)= A+ By +Cy^2 \\v(0) = 0\\v(75 \, mm) = 1.125 \, m/s\\v'(75 \, mm) = 0\\`

From the no-slip condition, we can deduce that
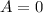`A=0` and so we are left with just two terms:

`v(y) = By + C y ^2 \\`

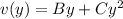
We know that the vertex is at
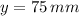`y= 75 \, mm` and so we can rewrite the last equation as:

`v(y) = k(y-75 \, mm) ^2+h`

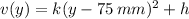
where k and h are constants to be determined. First we check that
`v( 75 \, mm) = 1.125 \,  m/s` :

`v( 75 \, mm) = k(75 \, mm -75 \, mm) ^2+h = h = 1.125 \, m/s\\\\h= v_(max) = 1.125 \,  m/s`

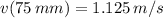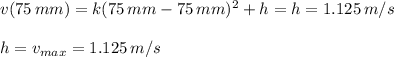
So we found that h was the maximum velocity for the fluid, now we have to determine k, for that we need to make use of the no-slip condition.

`v( 0) = k( -75 \, mm) ^2+  1.125 \,  m/s= 0 \quad (no \, \textendash slip)  \\\\k= - \cfrac{ 1.125 \, m/s }{(75 \, mm ) ^2} = - \cfrac{ 1125 \, mm/s }{(75 \, mm ) ^2}\\\\k= -  \cfrac{0.2}{mm * s}`

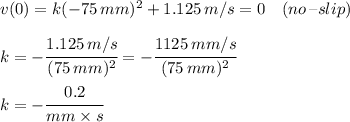
And thus we find that the final expression for the fluid's velocity is:

`v( y) = 1125-  0.2 ( y -75 ) ^2`

where v is in mm/s and y is in mm.

In SI units it would be:

`v( y) = 1.125-  200 ( y -0.075 ) ^2`

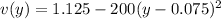
To calculate the shear stress, we need to take the derivative of this expression and multiply by the fluid's viscosity:

`\tau = \mu \cfrac{\partial v}{\partial y}`

`\tau =0.048\,   \cdot  (-400) ( y-0.075   )`

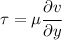
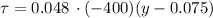
for
`y= 0.050 \, m` we have:

`\tau =0.048\,   \cdot  (-400) ( 0.050 -0.075   ) = 0.48\, Pa`

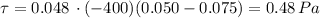
Which is our final result