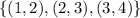Answer:
a)
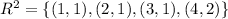
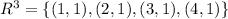
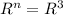 for every n>3
for every n>3
b)
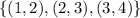
Explanation:
a)
From the definition of the relation we see that
R(1) = 1, R(2) = 1, R(3) = 2 and R(4) = 3
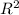 is the composite relation
is the composite relation
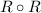
Let's compute it
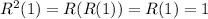
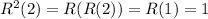
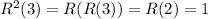
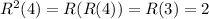
so
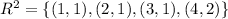
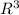 is computed in a similar way,
is computed in a similar way,

So we have
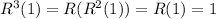
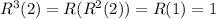
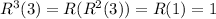
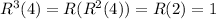
And
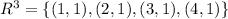
From here we see that
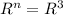
for every n>3
b)
We must look for the missing elements that would make R transitive, and those elements are