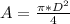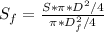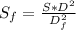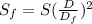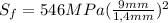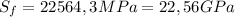Question

In a uniaxial tensile test, a steel specimen is stressed to the point of fracture at an engineering strength of 546 MPa, at which point the final diameter of the specimen is 1.4 mm. Given that the original diameter of the cylindrical specimen was 9 mm, determine: the true stress in GPa

Answer 1

`S_(f) = 22,56 GPa`

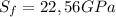
Step-by-step explanation:

In a uniaxial tensile test the engineering strength is calculated based on the original cross section of the specimen, during the test the strength is calculated based on the force measured:

(1)
`S = (F)/(A)`

Where:

S is the strength in MPa

F is the force measured in Newton

A is the original cross section area of the specimen in mm2

This is reasonably true when the deformation of the specimen is relatively small. But when the force applied to the specimen reaches the yield point of the material it starts deforming in a plastic manner, so the deformation of the specimen is no longer negligible. So the engineering calculation of the strength has an "error". The true stress at fracture point would be:

(2)
`S_(f) = (F_(f))/(A_(f))`

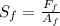
We can calculate the force from the strength solving equation 1 for F:

(3)
`F = S*A`

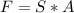
Replacing in (3):

(4)
`S_(f) = (S*A)/(A_(f))`

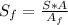
Given that the area of a round specimen is calculated by:

`A =(\pi * D^(2))/(4)`

`S_(f) = (S*\pi * D^(2) / 4)/(\pi * D_(f)^(2) / 4)`

`S_(f) = (S* D^(2) )/( D_(f)^(2) )`

`S_(f) = S ((D)/( D_(f)))^(2)`

`S_(f) = 546 MPa ((9 mm)/( 1,4 mm))^(2)`

`S_(f) =22564,3 MPa = 22,56 GPa`