Answer:
Steam condensation rate = 0.642 kg/s
Step-by-step explanation:
Given data:

L = H = 2m
b = 10 m
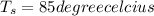
film temperature
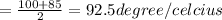
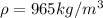

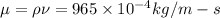
Pr = 1.92
Cp= 4208.12 J/kg K
K = 0.676
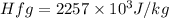
![h = 0.949[(k^3\rho^2 g Hfg)/(\mu l (T_(sat)_T_(s))]^(1/4)](https://img.qammunity.org/2020/formulas/engineering/college/i5bpysfdi2q5uiolgj4ltxcjq9mzp7mu8w.png)
![h = 0.946[(0.676^3* 965^2* 2257* 10^3)/(3.07* 10^(-4) * 2* (100-85))]^(1/4)](https://img.qammunity.org/2020/formulas/engineering/college/oovzg4orqa1lyx2h4fvcvygrhlojv13ac2.png)
solving for h we get
h = 4835.32 W/m^2 K
Heat transfer rate
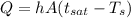
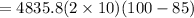
= 1450.74 kw
Steam condensation rate


= 0.642 kg/s