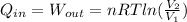Question

Consider the expansion of a gas at a constant temperature in a water-cooled piston-cylinder system. The constant temperature is achieved by controlled input of energy as heat Q to the gas. Treating the gas as idea, derive expressions for the energy output as work, W and energy input as heat, Q, as a function of the expansion ratio. (V2/V1)

Answer 1

`Q_(in) = W_(out) = nRT ln ((V_(2))/(V_(1)))`

Step-by-step explanation:

According to the first thermodynamic law, the energy must be conserved so:

`dQ = dU - dW`

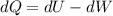
Where Q is the heat transmitted to the system, U is the internal energy and W is the work done by the system.

This equation can be solved by integration between an initial and a final state:

(1)
`\int\limits^1_2 {} \, dQ = \int\limits^1_2 {} \, dU - \int\limits^1_2 {} \, dW`

As per work definition:

`dW = F*dr`

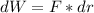
For pressure the force F equials the pressure multiplied by the area of the piston, and considering dx as the displacement:

`dW = PA*dx`

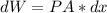
Here A*dx equals the differential volume of the piston, and considering that any increment in volume is a work done by the system, the sign is negative, so:

`dW = - P*dV`

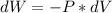
So the third integral in equation (1) is:

`\int\limits^1_2 {- P} \, dV`

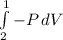
Considering the gas as ideal, the pressure can be calculated as
`P = (n*R*T)/(V)`, so:

`\int\limits^1_2 {- P} \, dV = \int\limits^1_2 {- (n*R*T)/(V)} \, dV`

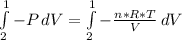
In this particular case as the systems is closed and the temperature constant, n, R and T are constants:

`\int\limits^1_2 {- (n*R*T)/(V)} \, dV = -nRT \int\limits^1_2 {(1)/(V)} \, dV`

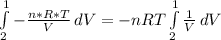
Replacion this and solving equation (1) between state 1 and 2:

`\int\limits^1_2 {} \, dQ = \int\limits^1_2 {} \, dU + nRT \int\limits^1_2 {(1)/(V)} \, dV`

`Q_(2) - Q_(1) = U_(2) - U_(1) + nRT(ln V_(2) - ln V_(1))`

`Q_(2) - Q_(1) = U_(2) - U_(1) + nRT ln (V_(2))/(V_(1))`

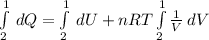
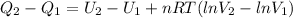
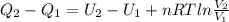
The internal energy depends only on the temperature of the gas, so there is no internal energy change
`U_(2) - U_(1) = 0`, so the heat exchanged to the system equals the work done by the system:

`Q_(in) = W_(out) = nRT ln ((V_(2))/(V_(1)))`