Answer:
a) 14.12psi, b) 390.86inH2O, d) 97.36kPa, d)12.42m
Step-by-step explanation:
In order to do the conversions we need to use conversion rates:
a) 1psi=2.03602inHg
so:
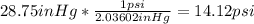
and the same procedure is used for parts b and d:
b) 1inHg=13.595inH2O
so:
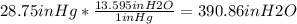
d) 1inHg=3.386kPa
so:
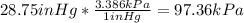
e)
Now part e is a little tricky since we need to review our specific gravity concept. The specific gravity is defined as the ratio between the specific weight of a substance ofver the specific weight of water.
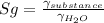
so when solving for the specific gravity of the substance, we get that it is:
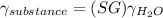
which can be used in the pressure equation:

when solving for h we get that:

when substituting equations we get that:
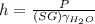
we know that:
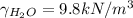
and from the previous part of the problem we know the pressure in kPa, so when using this data we get that:
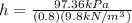
so:
h=12.42m