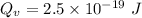Answer:
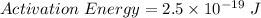
Step-by-step explanation:
Using the expression shown below as:
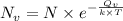
Where,
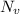 is the number of vacancies
is the number of vacancies
N is the number of defective sites
k is Boltzmann's constant =
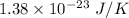
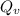 is the activation energy
is the activation energy
T is the temperature
Given that:
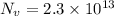
N = 10 moles
1 mole =
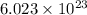
So,
N =
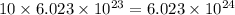
Temperature = 425°C
The conversion of T( °C) to T(K) is shown below:
T(K) = T( °C) + 273.15
So,
T = (425 + 273.15) K = 698.15 K
T = 698.15 K
Applying the values as:
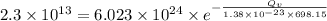
![ln[\frac {2.3}{6.023}* 10^(-11)]=-\frac {Q_v}{1.38* 10^(-23)* 698.15}](https://img.qammunity.org/2020/formulas/engineering/college/b1f2tggs0gzsr57zn25cd4xj42v4pahotf.png)