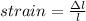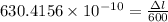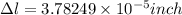Determine displacement (in) of a 1.37 in diameter steel bar, which is 50 ft long under a force of 27,865 lb if elasticity modulus is 30 x 100 psi. Make sure you do not round up …

Question

asked May 21, 2020 165k views

1 Answer

Jamix · Answer 1 · 2020-05-25T14:41:34+0000

Answer:

So displacement in inch will be
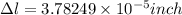
$\Delta l=3.78249* 10^(-5)inch$

Step-by-step explanation:

We have given length = 50 feet

We know that 1 feet = 12 inches

Force F = 27865 LB

Modulus of elasticity
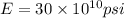
E=30* 10^(10)psi

So 50 feet = 50×12 = 600 inches

Diameter d = 1.37 inch

So radius
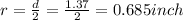
r=(d)/(2)=(1.37)/(2)=0.685inch

So area
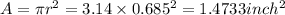
$A=\pi r^2=3.14* 0.685^2=1.4733inch^2$

We know that stress
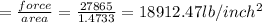
=(force)/(area)=(27865)/(1.4733)=18912.47lb/inch^2

Now we know that modulus of elasticity
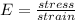
E=(stress)/(strain)

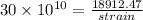
30* 10^(10)=(18912.47)/(strain)

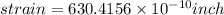
strain=630.4156* 10^(-10)inch

Now we know that
$strain=(\Delta l)/(l)$

$630.4156* 10^(-10)=(\Delta l)/(600)$

$\Delta l=3.78249* 10^(-5)inch$