Question

For normally (Gaussian) distributed data, what percentage of the data lies within 1.09 standard deviation(s) of the mean?

Answer 1

The percentage of the data that lies within 1.09 standard deviation(s) of the mean is 72.42%.

Step-by-step explanation:

The properties of the Normal Distribution have been thoroughly investigated for many years, which result in an advantage for solving problems concerning this distribution.

One of them is an important transformation of the original formula for the density function--and also applicable to the cumulative function--that permits us to obtain the same values for any distributed data that follow a Gaussian Distribution, irrespectively of the different means and standard deviations values.

This transformation is as follows:

`\\ z = ((x-\mu))/(\sigma)`

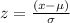
That is:

`\\ f(x) = (1)/(\sigma√(2\pi)) e^{( -(x-\mu)^(2))/(2\sigma^(2)) }`,

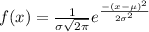is then, after transformation:

`\\ f(x) = (1)/(√(2\pi)) e^{-(z^(2))/(2)}`

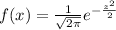
The density function of z is also normal with zero mean and standard deviation of 1.

It is also important to notice that the values of the standardized variable z give us 'how far' the value is from the mean of the distribution and to know that this distribution is symmetrical to both sides of the mean, too.

Thus, having gathered all this information, we can calculate what percentage of the data that lies within 1.09 standard deviations of the mean.

For
`\\ z = 1.09`, and
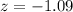`\\ z = -1.09`, due to symmetry of the normal distribution, we can consult the values for the cumulative distribution function corresponding to them, using tables in books, digital calculators or software available to calculate this.

For
`\\ z = 1.09= 0.8621`

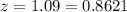
Because of the symmetry of the Normal Distribution, the value for
`\\ z = -1.09= 1-0.8621=0.1379`

So, the percentage of the data that lies within 1.09 standard deviations of the mean is:

0.8621 - 0.1379 = 0.7242 or 72.42% of the data.

According to the Empirical Rule, the percentage of data that lies within 1 standard deviation is 68.27%, within 2 standard deviations is close to 95% and 3 standard deviations 99.7%.

Considering that the value of z = 1.09 is slightly greater than z = 1, the result of 72.42% is reasonable compared to 68.27% for these values of z.