Question

The comet Churyumov-Gerasimenko has an unusual orbit for a comet. Instead of being far beyond Neptune like most comets, it is much closer to the Sun, and has a semi major axis of just 3.46 astronomical units (AU). Jupiter has a semi major axis of 5.20 AU. Based on Kepler’s 3rd law, does the comet orbit the Sun with a longer or shorter period than Jupiter?

Answer 1

comet has shorter period

Step-by-step explanation:

Given data:

comet semi major axis 3.46 AU

JUPITER major axis = 5.20 AU

We know that from kepler 3rd law, the square of orbital period is directly propotional to cube of semi-major axis of its orbit. i.e

`P^2 ∝ A^3`

`P^2 = K A^3`

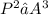
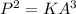
where K is constant =1

`P^2 =A^3`

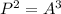
P - ORBITAL PERIOD (YR)

A - SEMI-MAJOR AXIS (AU)

For Jupiter

`P =√(A^3)`

`P = √(5.20^3) = 11.85 Yr`

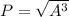
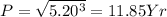
for Churyumov - Gerasimenko

`P = √(A^3)`

`P = √(3.46^3)`

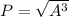
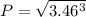
P = 6.43 Yr

Therefore comet has shorter period