Answer:
Choice (a) 1.4 J.
Step-by-step explanation:
The energy stored in one capacitor of capacitance
 at voltage
at voltage
 can be found with the equation
can be found with the equation
 .
.
If the voltages across each capacitor and their capacitance are known, it would be possible to find their energies separately. The total energy stored would equal to the sum of the two energies.
However, that's not the case for this particular question. Only the voltage across the two capacitors, combined, is given. It would potentially be helpful to consider the two capacitors as a combined one.
The effective capacitance
 of two capacitors
of two capacitors
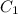 and
and
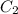 , connected in series, is similar to the effective resistance of two resistors connected in parallel:
, connected in series, is similar to the effective resistance of two resistors connected in parallel:
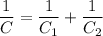 .
.
Equivalently,
 .
.
In this question,
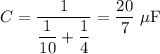 .
.
Note as long as both
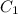 and
and
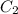 are in the same unit,
are in the same unit,
 will also be in that unit.
will also be in that unit.
Convert the unit of the effective capacitance to Faraday (derived SI-unit for capacitance.)
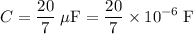 .
.
Find the energy in Joules (derived SI-unit for energy):
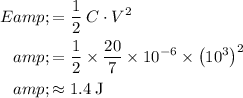 .
.