Answer:
(a). The wave length of 1 eV electron is
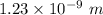 .
.
(b). The wave length of 10 MeV proton is
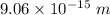 .
.
(c). The wave length of 100 MeV electron is
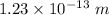 .
.
Step-by-step explanation:
Given that,
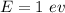
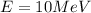
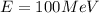
(a). We need to calculate the wavelength of 1 eV electron
Using formula of De Broglie wavelength
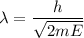
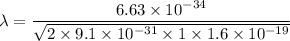
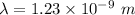
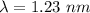
The wave length of 1 eV electron is
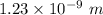 .
.
(b). We need to calculate the wavelength of 10 MeV proton
Using formula of De Broglie wavelength
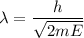
Put the value into the formula
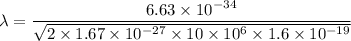
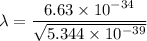
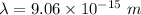
The wave length of 10 MeV proton is
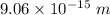 .
.
(c). We need to calculate the wavelength of 100 MeV electron
Using formula of De Broglie wavelength
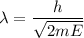
Put the value into the formula
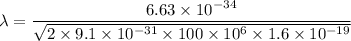
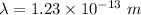
The wave length of 100 MeV electron is
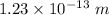 .
.
Hence, This is the required solution.