Answer:
a)
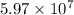 ms⁻¹
ms⁻¹
b)
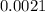 sec
sec
Step-by-step explanation:
(a)
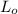 = Actual length of the vehicle = 50 m
= Actual length of the vehicle = 50 m
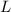 = length measured by the earthbound observer = 49 m
= length measured by the earthbound observer = 49 m
 = speed of the vehicle
= speed of the vehicle
 = speed of light = 3 x 10⁸ ms⁻¹
= speed of light = 3 x 10⁸ ms⁻¹
Length measured by the earthbound observer is given as
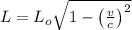
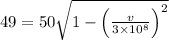
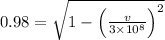
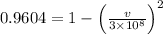
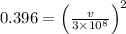
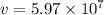 ms⁻¹
ms⁻¹
b)
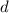 = distance traveled = 6000 km = 6 x 10⁶ m
= distance traveled = 6000 km = 6 x 10⁶ m
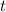 = time measured by a clock on the vehicle
= time measured by a clock on the vehicle
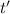 = time measured by a clock on the earth
= time measured by a clock on the earth
Time measured by a clock on the vehicle is given as
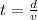
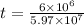
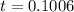 sec
sec
Time measured by a clock on the earth is given as
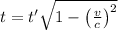
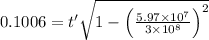
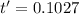 sec
sec
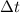 = time difference
= time difference
Time difference is given as
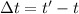
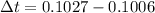
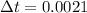
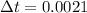 sec
sec