Question

Consider a disk of radius 2.6 cm with a uni- formly distributed charge of +6.7.1C. Compute the magnitude of the electric field at a point on the axis and 3.7 mm from the center. The value of the Coulomb constant is 8.98774 x 10 N m2/c

Answer 1

E=15.3*10¹³ N/C : approximate

Step-by-step explanation:

We use the following formula to calculate the electric field due to a disk with uniform surface charge at a point P that is along the central perpendicular axis of the disk and at a distance x from the center of the disk:

E= 2*π*k*σ*F Fórmula ( 1 )

`F= 1-\frac{x}{\sqrt{R^(2)+x^(2)  } }`

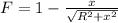
E: Electric field at point P (N/C)

σ: surface charge density (C/m²)

R: disk radio (m)

x :distance from the center of the disk to the point P located on the axis of the disk (m)

K: Coulomb constant ( N*m²/C)

Equivalences

1cm = 10⁻²m

1mm = 10⁻³m

Data

R =2.6 cm= 2.6*10⁻²m = 0.026m

x=3.7 mm = 3.7* 10⁻³m = 0,0037 m

Q=+6.71C.

k= 8.98774 * 10⁹ N* m²/C

Calculation of surface charge density (σ )

σ= Q/A

Q: uniformly distributed charge (C)

A: disk area (m²) = π*R²

σ= +6.71C/π*(2.6*10⁻²)²m² = 3159.56C/m²

Calculation of the electric field at point P

We apply formula (1) and replace data

E= 2*π*3159.56*8.98774*10⁹ *F

`F= 1-\frac{x}{\sqrt{R^(2)+x^(2)  } }`

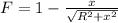
E=15.3*10¹³ N/C : approximate