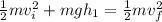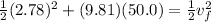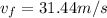Question

A ball is rolling along a road at the top of a hill, at a velocity of 10.0 km/hr. The ball rolls down a 50.0 m high hill. Neglecting air and road resistance, estimate the velocity of the ball at the bottom of the hill. Upload your solution.

Answer 1

`v_f = 31.44 m/s`

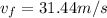
Step-by-step explanation:

initial height of the ball is given as

`H = 50.0 m`

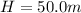
initial speed of the ball is given as

`v = 10.0 km/h`

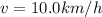
now we know that

`v = 10 * (1000)/(3600)`

`v = 2.78 m/s`

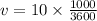
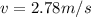
now by energy conservation we can say

initial kinetic energy + initial potential energy = final kinetic energy + final potential energy

`(1)/(2)mv_i^2 + mgh_1 = (1)/(2)mv_f^2`

`(1)/(2)(2.78)^2 + (9.81)(50.0) = (1)/(2)v_f^2`

`v_f = 31.44 m/s`