Question

Object A has a charge of +3.0 mC and Object B has a charge of -2.0 mC. Objects A and B are separated by a distance of 1.0e-10 m. If the objects are moved apart such that they have a separation of 2.0e-10 m, then by what factor will the electric force felt by each object change?

Answer 1

since the distance between two charges is double so the force between them is decrease by a factor of 1/4 times

Step-by-step explanation:

As we know that force between two charges is given as

`F = (kq_1q_2)/(r^2)`

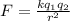
here we know that

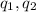`q_1, q_2` = magnitude of two charges

`r` = distance between two charges

since the electrostatic force between two charges is inversely depends on the square of the distance between two charges so as we increase the distance between two charges the force between the two charges will decrease

initially the two charges are placed at

`r_1 = 1.0 * 10^(-10) m`

`r_2 = 2.0 * 10^(-10)m`

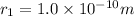
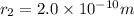
since the distance between two charges is double so the force between them is decrease by a factor of 1/4 times