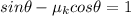Answer:
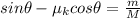
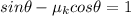
Step-by-step explanation:
Force of friction on M mass so that it will move down the inclined plane is given as
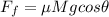
now if it is moving down the inclined plane at constant speed
so we will have

on other side the mass "m" will go up at constant speed
so we have
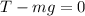
so we have
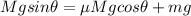
so we have
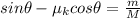
for special case when m = M
then we have