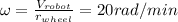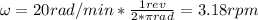Answer:
a) ω1 = 18rpm ω2 = -18rpm
b) ω1 = 102rpm ω2 = 138rpm
c) ω1 = ω2 = 3.18rpm
Step-by-step explanation:
For the first case, we know that each wheel will spin in a different direction but with the same magnitude, so:
ωr = 6rpm This is the angular velocity of the robot
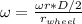 where D is 30cm and rwheel is 5cm
where D is 30cm and rwheel is 5cm
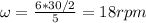 One velocity will be positive and the other will be negative:
One velocity will be positive and the other will be negative:
ω1 = 18rpm ω2 = -18rpm
For part b, the formula is the same but distances change. Rcircle=100cm:
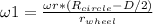
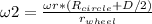
Replacing values, we get:
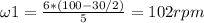
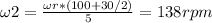
For part c, both wheels must have the same velocity: