Answer:
(a) 12.52 m/s
(b) 15.34 m/s
Step-by-step explanation:
mass, m = 34.9 kg
h = 16 m
(a) Initial velocity, u = 0
height = h / 2 = 16 / 2 = - 8 m (downward)
let the speed of child is v.
acceleration, a = - 9.8 m/s^2 (downward)
Use third equation of motion
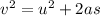
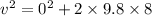
v = 12.52 m/s
(b) Initial velocity, u = 0
height = 3 h / 4 = 12 m = - 12 m (downward)
let the speed of child is v.
acceleration, a = - 9.8 m/s^2 (downward)
Use third equation of motion
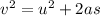
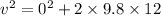
v = 15.34 m/s