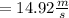Answer:
Speed of the ball in position D
Step-by-step explanation:
Given:
Position of B=11.3

Position of D=1.9

Velocity of B=6.2

To Find:
Velocity of D
Solution:
According to the formula, Velocity is given as
![V d=\sqrt{\left[V b^(2)+(2 * g * d y)\right]}](https://img.qammunity.org/2020/formulas/physics/middle-school/tiv2cw0d7v3pnygghsov8qzxpuvo7gty1n.png)
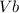 =Velocity of B
=Velocity of B
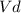 =Velocity of D
=Velocity of D
g=acceleration due to gravity=9.8 m/s^2
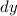 =Change in position of B and D
=Change in position of B and D
Substitute the all values in the above equation we get
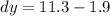
![V d=\sqrt{\left[6.2^(2)+(2 * 9.8 *(11.3-1.9))\right]}](https://img.qammunity.org/2020/formulas/physics/middle-school/kbkiggrsa2vfn3yomosbd8v37khd8kn1jj.png)
![=√([38.44+(2 * 9.8 *(9.4))])](https://img.qammunity.org/2020/formulas/physics/middle-school/lxkdgccezlzc5n5qs6cvbbd2736mahqan2.png)
![=√([38.44+(19.6 * 9.4)])](https://img.qammunity.org/2020/formulas/physics/middle-school/ufbgzkydhcgde0dxwb20yet6itq0pdcpw2.png)
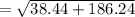
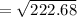
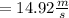
Result :
The velocity of D is