Question

Two spheres are cut from a certain uniform rock. One has radius 4.10 cm. The mass of the other is eight times greater.

Answer 1

8.2 cm

Step-by-step explanation:

mass of one sphere = m

mass of other sphere = 8 m

Radius of first sphere = r = 4.10 cm

let the radius of another sphere is R

As we know that mass = volume x density

Let the density of the rock is d.

density of rock remains same.

density of small sphere = density of big sphere

mass of small sphere / volume of small sphere =

mass of big sphere / volume of big sphere

`(m)/((4)/(3)\pi r^(3))=(8m)/((4)/(3)\pi R^(3))`

`R^(3)=8r^(3)`

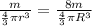
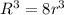
R = 2 r

R = 2 x 4.10 = 8.2 cm

Thus, the radius of big sphere is 8.20 cm.