Question

Derive the equation of the parabola with a focus at (−2, 4) and a directrix of y = 6. Put the equation in standard form.

f(x) = one fourthx2 − x + 4
f(x) = −one fourthx2 − x + 4
f(x) = one fourthx2 − x + 5
f(x) = −one fourthx2 − x + 5

Answer 1

B

Explanation:

From any point (x, y) on the parabola the focus and directrix are equidistant.

Using the distance formula

`√((x+2)^2+(y-4)^2)` = | y - 6 |

Squaring both sides

(x + 2)² + (y - 4)² = (y - 6)² ← distributing

x² + 4x + 4 + y² - 8y + 16 = y² - 12y + 36 ( subtract y² - 12y + 36 from both sides )

x² + 4x + 4 + 4y - 20 = 0 ( subtract x² + 4x + 4 from both sides )

4y - 20 = - x² - 4x - 4 ( add 20 to both sides )

4y = - x² - 4x + 16 ( divide through by 4 )

y = -
`(1)/(4)` x² - x + 4, that is

f(x) = -
`(1)/(4)` x² - x + 4 → B

Answer 2

Option B

Explanation:

Given that a parabola has a focus at (−2, 4) and a directrix of y = 6.

We have to find the equation of the parabola in std form

We know that a parabola is a conic section in which all points are equidistant from the focus and vertex.

Let (x,y) be any point on the parabola

Distance of (x,y) from the focus =
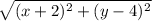`√((x+2)^2+(y-4)^2)` ...i

Distance of (x,y) from directrix = difference in y coordinate =
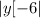`|y[-6|`...ii

Since i = ii, square and equate both

`(x+2)^2+(y-4)^2=(y-6)^2\\x^2+4x+4 -8y+16 = -12y+36\\4y=-x^2-4x+16\\y = (-1)/(4) d^2-x+4`

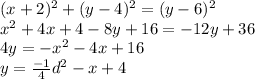
Hence option B is right.