Question

A man pushing a mop across a floor causes it to undergo two displacements. The first has a magnitude of 152 om and makes an angle of 110 with the positive xaxis. The resulta displacement has a magnitude of 131 cm and is directed at an angle of 38.0 to the positive axis. Find the magnitude and direction of the second displacement magnitude direction 1 (countercockwise from the positive x-axis)

Answer 1

D₂= 167,21 cm : Magnitude of the second displacement

β= 21.8° , countercockwise from the positive x-axis: Direction of the second displacement

Step-by-step explanation:

We find the x-y components for the given vectors:

i: unit vector in x direction

j:unit vector in y direction

D₁: Displacement Vector 1

D₂: Displacement Vector 2

R= resulta displacement vector

D₁= 152*cos110°(i)+152*sin110°(j)=-51.99i+142.83j

D₂= -D₂(i)-D₂(j)

R= 131*cos38°(i)+ 131*sin38°(j) = 103.23i+80.65j

We propose the vector equation for sum of vectors:

D₁+ D₂= R

-51.99i+142.83j+D₂x(i)-D₂y(j) = 103.23i+80.65j

-51.99i+D₂x(i)=103.23i

D₂x=103.23+51.99=155.22 cm

+142.83j-D₂y(j) =+80.65j

D₂y=142.83-80.65=62.18 cm

Magnitude and direction of the second displacement

`D_(2) =\sqrt{(D_(x))^(2) +(D_(y) )^(2)  }`

`D_(2) =\sqrt{(155.22)^(2) +(62.18 )^(2)  }`

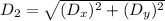
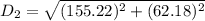
D₂= 167.21 cm

Direction of the second displacement

`\beta = tan^(-1) (D_(y))/(D_(x) )`

`\beta = tan^(-1) (62.18)/(155.22 )`

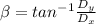
β= 21.8°

D₂= 167,21 cm : Magnitude of the second displacement

β= 21.8.° , countercockwise from the positive x-axis: Direction of the second displacement