Answer:
44.755 m
Step-by-step explanation:
Given:
Height of the movie star, H = 1.75 m = 1750 mm
Height of the image, h = - 8.25 mm
Focal length of the camera = 210 mm
Let the distance of the object i.e the distance between camera and the movie star be 'u'
and
distance between the camera focus and image be 'v'
thus,
magnification, m =
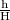
also,
m =
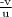
thus,
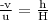
or
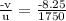
or
 ....................(1)
....................(1)
now, from the lens formula
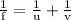
on substituting value from (1)

or

or
u = 210 × ( 1 + 212.12 )
or
u = 44755.45 mm
or
u = 44.755 m