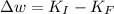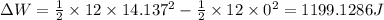Question

A particular automotive wheel has an angular moment of inertia of 12 kg*m^2, and is decelerated from 135 rpm to 0 rpm in 8 seconds. a. How much torque is required to do this? b. How much work is done to accomplish this?

Answer 1

(A) Torque required is 21.205 N-m

(b) Wok done will be equal to 1199.1286 j

Step-by-step explanation:

We have given moment of inertia
`I=12kgm^2`

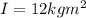
Wheel deaccelerate from 135 rpm to 0 rpm

135 rpm =
`135* (2\pi )/(60)=14.1371rad/sec`

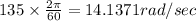
Time t = 8 sec

So angular speed
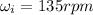`\omega _i=135rpm` and
`\omega _f=0rpm`

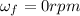
Angular acceleration is given by
`\alpha =(\omega _f-\omega _i)/(t)=(0-14.1371)/(8)=--1.7671rad/sec^2`

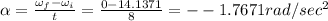
Torque is given by torque
`\tau =I\alpha`

`=12* 1.7671=21.205N-m`

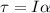
Work done to accelerate the vehicle is

`\Delta w=K_I-K_F`

`\Delta W=(1)/(2)* 12* 14.137^2-(1)/(2)* 12*0^2=1199.1286J`