Question

A bicyclist is finishing his repair of a flat tire when a friend rides by with a constant speed of 3.1 m/s . Two seconds later the bicyclist hops on his bike and accelerates at 2.4 m/s^2 until he catches his friend. a) How much time does it take until he catches his friend (after his friend passes him)?

Express your answer using two significant figures.

Answer 1

5.91 seconds

Step-by-step explanation:

t = Time taken

u = Initial velocity

v = Final velocity

s = Displacement

a = Acceleration

Distance = Speed × Time

⇒Distance = 3.1t

Distance traveled by bicycle that passes through = 3.1t

`s=ut+(1)/(2)at^2\\\Rightarrow s=0* t+(1)/(2)* 2.4* (t-2)^2\\\Rightarrow s=1.2(t-2)^2`

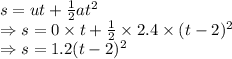
They both travel the same distance

`3.1t=1.2(t-2)^2\\\Rightarrow 31t=12\left(t-2\right)^2\\\Rightarrow 12t^2-79t+48=0`

`t=(79+√(3937))/(24),\:t=(79-√(3937))/(24)\\\Rightarrow t=5.91, 0.67`

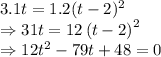
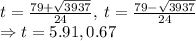
Hence, time taken by the bicyclist to catch the other bicyclist is 5.91 seconds