Answer:
Maximum speed, v = 36 m/s
Step-by-step explanation:
Given that,
The radius of the curved road, r = 120 m
Road is at an angle of 48 degrees. We need to find the maximum speed of stay on the curve in the absence of friction. On a banked curve, the angle at which it is cant is given by :
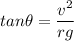
g is the acceleration due to gravity
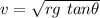
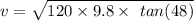
v = 36.13 m/s
or
v = 36 m/s
So, the maximum speed to stay on the curve in the absence of friction is 36 m/s. Hence, this is the required solution.