Answer:
x = 5 m ;approximate
Step-by-step explanation:
Kinematic equation for the object
Because the object moves with uniformly accelerated motion we apply the following equation:
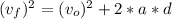
 : final speed ( m/s)
: final speed ( m/s)
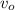 : initial speed ( m/s)
: initial speed ( m/s)
a: acceleration: ( m/s²)
d : distance (m)
Initial Conditions:
t₀=0 , x₀= 2.7 m, v₀= 4.3 m/s
x₀= inicial position
Final Conditions:
a= 5 m/s² , vf= 6.4 m/s
Calculation of the distance traveled by the object in final condition
We apply the formula (1)
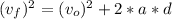
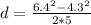
d= 2.247 m
Calculation of the final position :
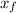
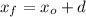
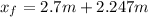
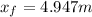
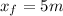 : approximate
: approximate