Question

A small silver (10.5 g/cm^3) cylinder of diameter 1.4 cm and a cylinder of lead (11.3 g/cm^3) balance each other when placed on a triple beam balance. If they have the same length, what must be the diameter of the lead cylinder?

Answer 1

The diameter of the lead cylinder is 1.35 cm.

Step-by-step explanation:

Given that,

Density of silver = 10.5 g/cm³

Density of lead = 11.3 g/cm³

Diameter = 1.4 cm

As mass of both is equal.

Let diameter of lead
`d_(l)`

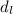
We need to calculate the the diameter of the lead cylinder

Using balance equation of density

`V* \rho_(s)=V* \rho_(l)`

`(\pi* d_(s)^2* h)/(4)*\rho_(s)=(\pi* d_(l)^2* h)/(4)*\rho_(s)`

`d_(l)^2=(d_(s)^(2)*\rho_(s))/(\rho_(l))`

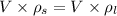
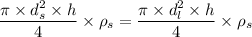
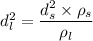
put the value into the formula

`d_(l)^2=((1.4*10^(-2))^2*10.5)/(11.3)`

`d_(l)=√(0.00018212)`

`d_(l)=0.0135\ m`

`d_(l)=1.35\ cm`

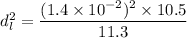
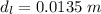
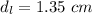
Hence, The diameter of the lead cylinder is 1.35 cm.