Answer:
(a). The potential on the negative plate is 42.32 V.
(b). The equivalent capacitance of the two capacitors is 0.69 μF.
Step-by-step explanation:
Given that,
Charge = 10.1 μC
Capacitor C₁ = 1.10 μF
Capacitor C₂ = 1.92 μF
Capacitor C₃ = 1.10 μF
Potential V₁ = 51.5 V
Let V₁ and V₂ be the potentials on the two plates of the capacitor.
(a). We need to calculate the potential on the negative plate of the 1.10 μF capacitor
Using formula of potential difference
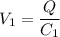
Put the value into the formula
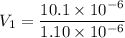
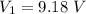
The potential on the second plate
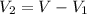
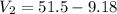
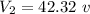
(b). We need to calculate the equivalent capacitance of the two capacitors
Using formula of equivalent capacitance
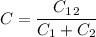
Put the value into the formula
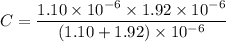
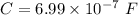
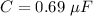
Hence, (a). The potential on the negative plate is 42.32 V.
(b). The equivalent capacitance of the two capacitors is 0.69 μF.