Question

Two projectile launchers are beside one another on level ground. Both launchers are directed at the same angle with respect to ground. Projectile A is launched with an initial speed v, and projectile Bis launched with an initial speed 2v. How do the ranges of the two projectiles compare with one another? (a) Projectile B will travel 4 times as far as projectile A prior to landing (b) Projectile B will travel 3 times as far as projectile A prior to landing (c) Projectile B will travel twice as far as projectile A prior to landing (d) Projectile B will travel 2.5 times as far as projectile A prior to landing

Answer 1

(a) Projectile B will travel 4 times as far as projectile A prior to landing

Step-by-step explanation:

Initial velocity = v

Angle at which the projectile is shot at = θ

g = Acceleration due to gravity

Range of a projectile is given by

`R=\frac {v^(2)\sin 2\theta}{g}`

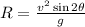
When Initial velocity = v

`R_A=(v^(2)\sin 2\theta)/(g)`

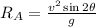
When Initial velocity = 2v

`R_B=((2v)^(2)\sin 2\theta)/(g)\\\Rightarrow R_B=(4v^2\sin 2\theta)/(g)`

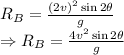
Dividing the equtions, we get

`(R_A)/(R_B)=((v^(2)\sin 2\theta)/(g))/((4v^2\sin 2\theta)/(g))`

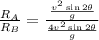
Here, the angle at which the projectiles are fired at are equal.

`(R_A)/(R_B)=(1)/(4)\\\Rightarrow R_B=4R_A`

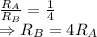
Hence, projectile B will travel 4 times as far as projectile A prior to landing