Answer:
The kangaroo was 1.164s in the air before returning to Earth
Step-by-step explanation:
For this we are going to use the equation of distance for an uniformly accelerated movement, that is:
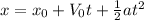
Where:
x = Final distance
xo = Initial point
Vo = Initial velocity
a = Acceleration
t = time
We have the following values:
x = 1.66m
xo = 0m (the kangaroo starts from the floor)
Vo = 0 m/s (each jump starts from the floor and from a resting position)
a = 9.8 m/s^2 (the acceleration is the one generated by the gravity of earth)
t =This is just the time it takes to the kangaoo reach the 1.66m, we don't know the value.
Now replace the values in the equation
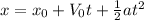
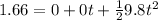

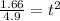

It takes to the kangaroo 0.582s to go up and the same time to go down then the total time it is in the air before returning to earth is
t = 0.582s + 0.582s
t = 1.164s
The kangaroo was 1.164s in the air before returning to Earth