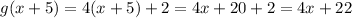Question

For f(x)= x+5 and g(x)=4x+2
find (fog)(x) And (gof)(x)

Answer 1

Composing functions means that the input of the outer functions is the output of the inner function.

In fact, you can rewrite the circle notation as

`(f\circ g)(x)=f(g(x)),\quad (g\circ f)(x)=g(f(x))`

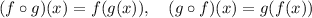
So, we can substitute g(x) with its expression:

`(f\circ g)(x)=f(g(x))=f(4x+2)`

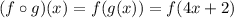
And since f(x)=x+5, we simply have to add 5 to its input:

`f(4x+2)=(4x+2)+5=4x+7`

Similarly, we have, substituting f with its expression,

`(g\circ f)(x)=g(f(x))=g(x+5)`

And since g(x)=4x+2, we have to multiply the input by 4 and add 2:

`g(x+5)=4(x+5)+2=4x+20+2=4x+22`