Answer:
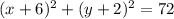
Explanation:
We are given the following information in the question:
y intercept = 4, -8
The circle passes through the point (-12, -8)
Equation of circle:

where r is the radius of circle, (h,k) is the center of circle.
The circle passes through the points (0,4), (0,-8_ and (-12,-8)
Putting these points in the equation of circle we get:
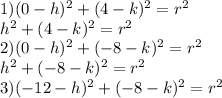
Now, we have three equations in three variables.
Solving the three equations, we obtain:
h = -6, k = -2, r =
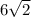
Putting these values in the equation of circle:
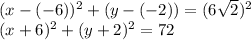
The above equation is the required equation of circle.