Question

Miriam is picking out some movies to rent, and she is primarily interested in comedies and foreign films. She has narrowed down her selections to 10 comedies and 15 foreign films. How many different combinations of 3 movies can she rent if she wants at least two comedies?

Answer 1

There are 795 combinations.

Explanation:

The number of ways or combinations in which we can select k element from a group of n elements is given by:

`nCk=(n!)/(k!(n-k)!)`

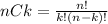
So, if Miriam want to choose 3 movies with at least two comedies, she have two options: Choose 2 comedies and 1 foreign film or choose 3 comedies.

Then, the number of combinations for every case are:

1. Choose 2 Comedies from the 10 and choose 1 foreign film from 15. This is calculated as:

`10C2*15C1=(10!)/(2!(10-8)!)*(15)/(1!(15-14)!)`

`10C2*15C1=675`

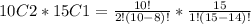
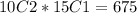
2. Choose 3 Comedies from the 10. This is calculated as:

`10C3=(10!)/(3!(10-3)!)=120`

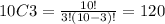
Therefore, there are 795 combinations and it is calculated as:

675 + 120 = 795