Question

A researcher reports that the time (in minutes) it takes children who are "picky eaters" to finish their vegetables is negatively skewed, with children finishing their vegetables in 4.2±1.0 (M±SD) minutes. Based on Chebyshev's theorem, we can conclude that68% of children finished their vegetables in 3.2 to 5.2 minutes.50% of children finished their vegetables in at least 3.2 minutes.99.7% of children finished their vegetables in 2.2 to 6.2 minutes.At least 89% of children finished their vegetables in 1.2 to 7.2 minutes.

Answer 1

Option d) Chebyshev's rule

Explanation:

The Chebyshev's rule state that for a data that is not distributed normally,

atleast
`(1 - (1)/(k^2))\% \text{ of data lies within the interval}~(Mean \pm (k)Standard ~Deviation)`.

Here, k cannot be 1 and is always greater than 2.

For k = 2,

`(1 - (1)/(4))* 100\% = 75\%` of data lies within the range of
`(\mu \pm 2\sigma)`

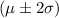
Atleast 75% of children finished their vegetables in
`(\mu \pm 2\sigma) = (4.2 \pm (2)1.0) = (2.2,6.2)`

For k = 3,

`(1 - (1)/(9))* 100\% = 88.912\%` of data lies within the range of
`(\mu \pm 3\sigma)`

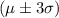
Atleast 89% of children finished their vegetables in
`(\mu \pm 3\sigma) = (4.2 \pm (3)1.0) = (1.2,7.2)`

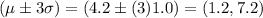
Thus, option d) is correct.