Question

(1 point) A street light is at the top of a 25 ft pole. A 4 ft tall girl walks along a straight path away from the pole with a speed of 6 ft/sec. At what rate is the tip of her shadow moving away from the light (ie. away from the top of the pole) when the girl is 45 ft away from the pole?

Answer 1

`(dx)/(dt)=7.14m/s`

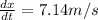
Step-by-step explanation:

As is showed at the figure annexed, we can solve this problem finding the relation between the girl displacement and the shadow displacement.

Relation the triangles (see figure annexed):

`(x)/(H)=(x-y)/(h)\\x=(H)/(H-h)y`

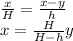
We derive in order to find the speed of the shadow, because:

dx/dt: shadow's speed

dy/dt: girl's speed

`(dx)/(dt) =(25)/(25-4)*6=7.14m/s`