Finally, we'll drag the corresponding domain description into the box under each graph based on our analysis.
- For the first graph, drag "all real numbers".
- For the second graph, drag "all real numbers except
 and
and
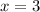 ".
". - For the third graph, drag "all real numbers between -3 and 3".
To answer the question presented in the image, we need to match each graph with its corresponding domain. Here's how to determine the domain for each graph step by step:
1. Examine the first graph:
- Look at where the graph exists along the x-axis.
- If the graph covers the entire x-axis without any breaks, then the domain is all real numbers.
- If there are breaks or gaps, note the intervals where the graph does not exist.
2. Examine the second graph:
- Repeat the process, looking for gaps along the x-axis.
- Check if the graph is only above or below the x-axis to see if it's only positive or negative real numbers.
- Look for vertical lines that the graph might approach but not touch (asymptotes), which would indicate values that are not included in the domain.
3. Examine the third graph:
- Again, look for any breaks along the x-axis.
- Determine if the graph is bounded within a certain range on the x-axis.
Now, let's apply this process to each graph in the uploaded image:
- First Graph: The graph covers all x-values without any breaks, so its domain is "all real numbers".
- Second Graph: The graph has a break at
 and
and
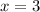 , so the domain is "all real numbers except
, so the domain is "all real numbers except
 and
and
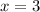 ".
". - Third Graph: The graph exists only between
 and
and
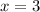 , so the domain is "all real numbers between -3 and 3".
, so the domain is "all real numbers between -3 and 3".