Question

Every day, there are 3 times more likes on an internet video of a cat which is modeled by the function c(n) = (3)n − 1, where n is the number of days since the video posted. On the first day, there were 143 likes. What is the function that shows the number of likes each day?

A. c(n) = (3)(143)^{n-1}
B. c(n) = 143^{n-1}
C. c(n) = (3)143 − n
D.143(3)^{n-1}

Answer 1

Answer: Hi! the answer is D, now let's prove it:

Ok, let's analyze our problem; we know two facts:

1) the first day, the video has 143 likes

2) each day that pases, there are 3 times more likes.

this means, that the day 1, the video has 143 like, the day 2, has 3*143 = 429 likes, the day 3, it has 3*429 = 1287

now, this is f(n) = the number 143 multiplied by 3 (n - 1) times, where n is the amount of days.

the function that describes this is f(n) =
`143*3^(n -1)`

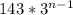
when n = 1, f(1) =
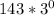`143*3^(0)` = 143

when n = 2, f(2) =
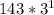`143*3^(1)` = 143*3

and so on, so the correct answer is D.

Also you can check the other functions if you like:

A) c(1) = (3)(143)^{1-1} = 3, so A doesn't work for the first day.

B) c(1) = 143^{1-1} = 1, B neither works for the first day.

C) c(1) = (3)143 − 1 = 428. C neither works for the first day