Question

A street light is at the top of a 25 ft pole. A 4 ft tall girl walks along a straight path away from the pole with a speed of 6 ft/sec. At what rate is the tip of her shadow moving away from the light (ie. away from the top of the pole) when the girl is 45 ft away from the pole?

Answer 1

Tip of the shadow of the girl is moving with a rate of 7.14 feet per sec.

Explanation:

Given : In the figure attached, Length of girl EC = 4 ft

Length of street light AB = 25 ft

Girl is moving away from the light with a speed = 6 ft per sec.

To Find : Rate (
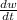`(dw)/(dt)`) of the tip (D) of the girl's shadow (BD) moving away from th

light.

Solution : Let the distance of the girl from the street light is = x feet

Length of the shadow CD is = y feet

Therefore,
`(dx)/(dt)=6` feet per sec. [Given]

In the figure attached, ΔAFE and ΔADE are similar.

By the property of similar triangles,

`(x)/(21)=(x+y)/(25)`

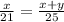
25x = 21(x + y)

25x = 21x + 21y

25x - 21x = 21y

4x = 21y

y =
`(4x)/(21)`

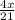
Now we take the derivative on both the sides,

`(dy)/(dt)=(4)/(21)* (dx)/(dt)`

=
`(4)/(21)* 6`

=
`(8)/(7)`

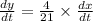
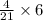
≈ 1.14 ft per sec.

Since w = x + y

Therefore,
`(dw)/(dt)= (dx)/(dt)+(dy)/(dt)`

`(dw)/(dt)=6+1.14`

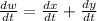
= 7.14 ft per sec.

Therefore, tip of the shadow of the girl is moving with a rate of 7.14 feet per sec.