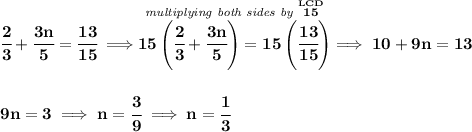Question

How would I solve 2/3+3n/5=13/15

Answer 1

well, one way to go about it is, to do away with the denominators by using the LCD of all fractions, hmmm let's see, we have denominators of 3,5 and 15, so the LCD will just be 15.

now let's multiply both sides by the LCD of 15 to do away with the denominators,

`\bf \cfrac{2}{3}+\cfrac{3n}{5}=\cfrac{13}{15}\implies \stackrel{\textit{multiplying both sides by }\stackrel{LCD}{15}}{15\left( \cfrac{2}{3}+\cfrac{3n}{5} \right)=15\left( \cfrac{13}{15} \right)}\implies 10+9n=13 \\\\\\ 9n=3\implies n=\cfrac{3}{9}\implies n = \cfrac{1}{3}`