Answer : The value of
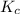 at this temperature is 0.0184
at this temperature is 0.0184
Explanation : Given,
Concentration of
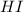 at equilibrium =
at equilibrium =
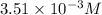
Concentration of
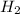 at equilibrium =
at equilibrium =
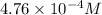
Concentration of
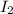 at equilibrium =
at equilibrium =
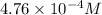
The given equilibrium reaction is,
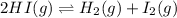
The expression of
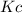 will be,
will be,
![K_c=([H_2][I_2])/([HI]^2)](https://img.qammunity.org/2020/formulas/chemistry/high-school/2jbk0j0rittzj3h568cub8sgelsd4a0jtr.png)
Now put all the given values in this expression, we get:
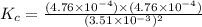
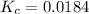
Therefore, the value of
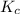 at this temperature is 0.0184
at this temperature is 0.0184