Answer : The freezing point of solution is 273.467 K
Explanation : Given,
Mass of glucose (solute) = 0.3 g
Mass of water (solvent) = 1000 g = 1 kg
Moles of fructose (solute) = 0.5 mol
Mass of water (solvent) = 1000 g = 1 kg
Molar mass of glucose = 180 g/mole
First we have to calculate the moles of glucose.
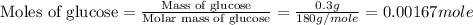
Now we have to calculate the total moles after mixing.
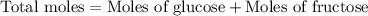
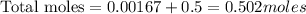
Now we have to calculate the molality.
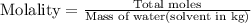

Now we have to calculate the freezing point of solution.
As we know that the depression in freezing point is a colligative property that means it depends on the amount of solute.
Formula used :
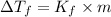
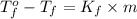
where,
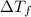 = change in freezing point
= change in freezing point
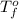 = temperature of pure water =
= temperature of pure water =

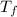 = temperature of solution = ?
= temperature of solution = ?
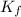 = freezing point constant of water =
= freezing point constant of water =
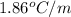
m = molality = 0.251 mole/kg
Now put all the given values in this formula, we get
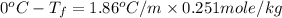
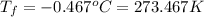
conversion used :
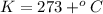
Therefore, the freezing point of solution is 273.467 K