Step-by-step explanation:
The given data is as follows.
Boiling point of water (
 = (100 + 273) K = 323 K,
= (100 + 273) K = 323 K,
Boiling point of solution (
 = (101.24 + 273) K = 374.24 K
= (101.24 + 273) K = 374.24 K
Hence, change in temperature will be calculated as follows.
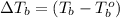
= 374.24 K - 323 K
= 1.24 K
As molality is defined as the moles of solute present in kg of solvent.
Molality =

Let molar mass of the solute is x grams.
Therefore, Molality =

m =

=
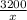
As,
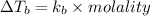
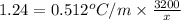
x =

= 1321.29 g
This means that the molar mass of the given compound is 1321.29 g.
It is given that molecular formula is
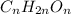 .
.
As, its empirical formula is
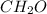 and mass is 30 g/mol. Hence, calculate the value of n as follows.
and mass is 30 g/mol. Hence, calculate the value of n as follows.
n =
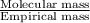
=
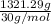
= 44 mol
Thus, we can conclude that the formula of given material is
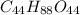 .
.